On explaining links between monetary policy and interest rates [fluff piece]

The main idea: modeling an inclined line whose angle is the interest rate and whose starting and ending points are monetary circulation volumes now and in the future explains a slew of otherwise peculiar relationships between interest rates and monetary policy. 

0. Posts on this blog are ranked in decreasing order of likeability to myself. This entry was originally posted on 09.12.2021, and the current version may have been updated several times from its original form.

0.1 This post is a fluff piece, containing analysis and commentary but no proposed solution to some issue. I try to keep this sort of stuff to a minimum as commentary for commentary’s sake is not the point of this blog.

 

1. Setting the true risk-free interest rate

1.1 Here’s a thought experiment. Suppose the monetary authority (and it can only be the monetary authority) decides to issue consols, bonds that will pay out a set amount every month forever. It sets the price and – this is crucial – commits to sell and buy back any quantity of these at this price, forever and ever. A fiat issuer can do this credibly, and no one else can. What would happen?

1.2 I reckon there would be a massive reshuffling of the entire structure of outstanding financial promises in the entire economy, such as to match the interest rate implicitly set by the new instrument. Once equilibrium is restored, this rate will be in force at all maturities. Let’s assume the rate is thus set at 2%.

1.3 Now, lets stop a moment and examine such an equilibrium. What does it mean for what I call the true risk-free rate to be at 2%? I say it means that the market now expects the volume of monetary circulation to grow at 2% p.a. forever. How else would anyone willing be able to invest into a sure 2% return forever unless the money is there to pay for this?

1.31 Even those left unimpressed by the jump in 1.3 would perhaps agree to park their disbelief for the moment, and review the ramifications of assuming some truth there. Perhaps the world that would result would be not too dissimilar from ours.

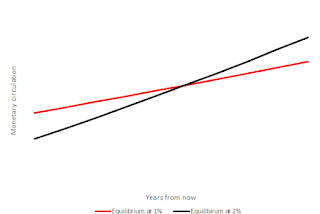
1.4 So, the expected behavior of circulation should look a bit like this.

1.5 Now, forever growth at 2% is set by the free buying and selling of the new instrument (but see section 5 on a key assumption here), but the current level of monetary circulation isn’t. If, say, velocity collapses due to any reason, the current circulation would go down (nothing stopping it).

1.6 Now, people would transact the instrument such as to return the expected path of circulation growth to 2%, resulting in a new equilibrium, lower than the original one across all horizons.

1.7 Now for a more interesting scenario. What happens in the monetary authority decides to lower the true risk-free rate by upping the price at which the instrument is issued and bought back? People can now sell back the same stream of money for a greater price, and marginal holders will sell back their consols, and get money in return. So, the interest rate falls but the money supply in this moment increases. The trajectory of circulation “pivots” around a point somewhere in the future. Where exactly does not matter, what matters is that the pivot point is not the present.

1.8 In a sense, what has happened here is that money expected in the future was “brought back” in the present, as at the lower rate it was not worth waiting. When the rate increases, the curve pivots the other way, lowering circulation now but increasing expected circulation in the future, “sending money into the future”.

1.9 To recap, in an economy where such an instrument is freely traded, the expected path of growth in circulation is set by the true risk-free rate. Whilst the setup does not prevent unexpected shifts in the current circulation due to velocity or base changes, the system has a tendency to limit the effect of such changes by “distributing” the shock in the future, such as to defend the rate. A change in the rate allows for the expected path of circulation growth to pivot around a point in the future: rate increases lower circulation now, but increase it in the future, and vice versa.

2. Modeling the fiat economy

2.1 Here’s the banger: this thought experiment produces predictions that are as valid in any modern economy, regardless of the lack of monetary-policy-by-consol. When modern central banks set interest rates, a chain of causation is initiated that allows these changes to percolate across the entire economy, through intermediaries such as banks.

2.2 The public may not be able to buy risk-free consols, but we bank with institutions who are able to access instruments that are almost equivalent. The thought experiment models reality to a decent extent, and so the predictions it makes stand.

2.3 What predictions are these? Can they help shed light on some weird link between monetary policy and interest rates? Yep.

2.4 Here’s a few predictions. Lowering interest rates increase monetary circulation now. Check, lowering rates is what you do when you need to give the economy a boost.

2.5 Here’s a second: increasing interest rates cuts inflation now. Indeed, by lowering the volume of circulation here and now. But higher rates are (seemingly confusingly) associated with high inflation! How? Easy, raising rates really does lower circulation now, but once expectations adjust it increases the rate at which the now-lower volume will increase. So, you trade less inflation now for more in the future!

2.6 Here’s a third: successive lowerings of the rate to jump-start the economy eventually lead to a liquidity trap. Yep, lowering rates increases circulation now, but once the market adjusts it realizes that the rate at which the volume will increase is now lower. You will need another shot to address the anemic growth, and then another, and then another. After each shot, the rate at which circulation is expected to grow diminishes, eventually leading to a situation where no further cuts are possible, even though they are needed more than ever. In other words, lowering rates is bringing money from the future to the present, and one eventually runs out of future money.

2.7 A fourth: an abnormal maturity curve, one where rates at higher maturities are lower than rates at lower maturities, indicates a lack of credibility of the monetary authority in the marketplace. “We don’t think you’ll be able to keep printing to the degree you are now, we forecast contraction”. Hence, collapse.

2.8 I could go on but I think the basics are clear. I propose that there isn’t a single initially puzzling relation between monetary policy and interest rates that this simple model does not explain, from the examples above to the otherwise weird behavior of exchange rates overshooting. 

3. The first test: escaping the liquidity trap

3.1 How about a real prediction that can be falsified?

3.2 Here it is: how to reliably get out of a liquidity trap in an afternoon. Say we have lowered rates so much in the past, that there is nowhere else to pivot, no more future money to pilfer now. Even worse, the low tilt of the path of circulation limits the degree to which the economy is able to absorb and disperse random shocks to the current volume of circulation. You know who you are.

3.3 We have to somehow pivot the curve back up without lowering current circulation, so just raising rates won’t cut it.

3.4 So, you raise the interest rate by the same amount you want to uplift inflation but at the same time instituting a half-peg to a major foreign currency, promising to sell as much local currency as needed to anyone who will take the current price as of the announcement. No buy-backs though. The peg will not allow the monetary volume to fall now, pivoting the path now, not in the future. We are creating money, and sending some back into the future too!

3.5 Done, your printing press will run so hot that you’ll be out of the trap by the end of the day.

3.6 Now, this will obviously only work if the peg is unexpected, otherwise the market will already have priced this in the rate, pre-emptively lowering circulation even before you raise rates. Worst of both worlds! So, a dangerous maneuver that relies on surprise.  

3.7 Still, others may think of better ways to stop monetary circulation from falling here and now once you raise rates. But if this is done, raising rates will surely get you out of any liquidity trap, and get inflation to wherever you need it to be. 

4. The second test: Lowering inflation at less risk of recession 

4.1 When inflation get above the point that can be tolerated, you raise rates and often cause a recession. Now, raising rates will lower monetary circulation now (hence lowering inflation) but increase the expected rate of increase in the future, so at some point you will need to do this again.

4.2 One may postulate that the recession is caused by the unforeseen crash in current circulation, instead of the rate raise itself, so is there a way to lower inflation without crashing the party?

4.3 Reverse the little maneuver of section 3: now you lower rates (ideally by the same degree you wish to lower inflation, but there are complications below) and be ready to spend reserves to buy back the flood of money coming you way. 

4.4 Now, reserves are not infinite, so there may be a limit to how much of a circulation increase you can safely absorb, hence a limit to how much you may lower rates. Unlike creating inflation, fighting inflation costs real resources. So go and stop, wait for reserves to replenish, then go again, and so on.

4.5 Ideally, you have both prevented the collapse of circulation now (hence a recession) and ensured inflationary expectations are lowered for good, by however much you can afford to cut you rates.

4.6 There is a very real risk here though, that you cannot control velocity. Seeing a rate cut in the face of inflation may well spook the market and have velocity go into overdrive, causing a much larger increase in current circulation than originally expected (remember, nothing stopping exogenous drops or jumps in velocity in this model).

4.7 This risk may be even exacerbated as the public sees reserves dwindle, in turn causing yet another jump in velocity, which requires yet more buybacks, and so on until the central bank's assets are depleted. 

4.8 All in all, a much more risky trick than getting out of a liquidity trap.

5. The third and real test: defending a rate

5.1 An implicit but absolutely key assumption of this model is that the central bank does not need to expend or acquire reserves to defend any rate it wishes to establish, above and beyond what may need to be expended or acquired in the first moment whilst marked expectations are being changed to suit the new rate. I.e. whilst the real rate is exogenous and set by the market, the nominal rate can be set as the Central Bank desires, and will require no continued intervention once the inflationary expectations change such as to square the nominal and real rates.

5.2 Once established, the rate is self-sustaining, which is how this model can assume you can control the rate and the base independently of one another.

5.3 If, on the other hand, practice is for the OMO desk to continuously and systematically go to market to defend whichever rate the bank has decided to enforce, and so you can only set one among the rate and the amount of real assets you buy or sell, the model belongs in the trash heap.  

5.4 So, which one is it? Do central banks see their assets grown to infinity if the rate they target is a basis point above the natural rate, or are rate cuts a popular way to cut inflation precisely because they cost next to nothing in terms of assets? I honestly do not know, but here's a prediction that is easy to falsify in a single sentence.

6. Addendum

6.1 Although it wouldn't be my go-to, I think you actually can run a responsive but fully automatic monetary policy based on issuing and fixing the price of consols alone, as per section 1. The only additional step to take would be to sterilize all incoming our outgoing cash flows to fight against those exogenous changes in circulation now. So, you promise to buy and sell whatever sum of consols at a given price and if, at the end of any given month, you find a net inflow of funds, you issue these back out through the foreign exchange, and the other way around. Now you should have fully set expectations of monetary growth that cannot be subject to exogenous shocks.  Still like this other system better.