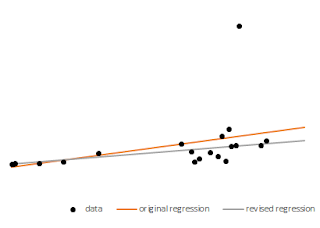
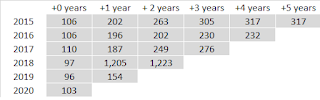On rank-ordering very complex datasets

The main idea: the concept of the efficient frontier can be generalized such as to allow the rank-ordering of extremely complex datasets based on a large set of mutually contradicting criteria. 0. Posts on this blog are ranked in decreasing order of likeability to myself. This entry was originally posted on 24.01.2022, and the current version may have been updated several times from its original form. 1.1 Say you have a list of things you’d like to compare with regards to a number of criteria. Obviously, if all things are such as to be ranked in the same order across all of these criteria, comparisons are easy. What to do when entities are ranked differently with regards to different criteria though? 1.2 To make this less esoteric, let’s take a simple example: I wish to purchase a used vehicle, and the only relevant considerations are its price (the lower the better), its production year (the more recent the better) and its mileage (the lower the better). I have this narro...