On removing abnormal claims from reserving triangles
The main idea: iteratively replacing the highest deviating
cell in a reserving triangle with the expected result for that cell removes
without ignoring abnormally large claims.
0. Posts on this blog are ranked in decreasing order of likeability to myself. This entry was originally posted on 27.10.2021, and the current version may have been updated several times from its original form.
1.1 In a previous post I discussed a general method for removing outliers from a dataset given that one has a model. Let's try now to apply this to non-life claims reserving by triangles.
1.2 The cumulated
triangle below includes one obvious outlier incurred in 2018, and emerging one
year after.
1.4 Let’s
work with basic chain ladder instead. Now, we could use year 0 claims as a
measure of exposure and the cumulated development factors as a pattern, but
this would mean that we always “take for granted” that year zero data.
1.5 A better
approach is to use the ultimate development as exposure. You can go about
calculating the ultimate by the usual longish fashion, or you can use a
shortcut as below, where you go by iteration calculating the ultimate development
of the earlier to the latter years, with the ultimate development of the earliest
year just being that year’s final datapoint (assume tails away).
1.6 The next
ultimate then is, if we stick to the color scheme below, BLUE = YELLOW x SUM OF
GREEN / SUM OF ORANGE. Iterative procedure but will give you the ultimates rather quicker than going through the dev factors drama.
1.7 Next we
use the ultimates (our measure of exposure) to derive the pattern, which is
just the sum of cumulated development at each interval divided by the sum of
exposure, in like fashion to the additive method. If you really miss your development factors, you can derive them easily from the pattern by dividing successive terms (or all terms by the first one if you need cumulative factors).
1.8 Now we
have the model of the triangle, and we can create a “synthetic” triangle by multiplying
exposure and pattern.
1.9 Next,
we calculate the absolute difference between the actual and synthetic triangles,
and isolate the greatest such difference. In this case, this will be a difference of $
202 between the synthetic value of $ 299 and the real value of $97 in the first
development year of 2018.
1.10 Now
Replace the 97 in the original triangle with the 299 in the synthetic and
re-run all calcs. By all I mean all, exposure, pattern, synthetic triangle,
differences, replace the sore thumb.
1.11 Repeat until the greatest difference between the two triangles is arbitrarily small. You get this
1.12 Notice
how the procedure has not changed the leading edge of the triangle, i.e. does
not change the amount of development experienced (if you use a cumulative triangle, which you should).
1.13 What has
changed is when this development appears, which is obvious if you look at the
difference in development pattern, where the obvious outlier in the original triangle
was making it look as if only 21% of the total development was done by year
zero (smoothed figure closer to 40%). 40% of development in year zero is close
to the 38% average of all years except the 2018 outlier.
1.14 What I really like about this application is that it gives me a way to use the full claims history without having to make a judgement call on what to consider big or abnormal claims. Chuck it all in there, God will recognize his own.
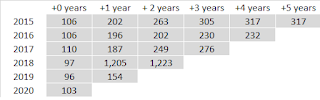




Comments
Post a Comment